Tutorials References Exercises Menu
HTML and CSS Computers Windows OS Cisco Networking Ms-Office Ms-SQL Server English Language

Zeal For Wisdom

Computer Number System

Number System

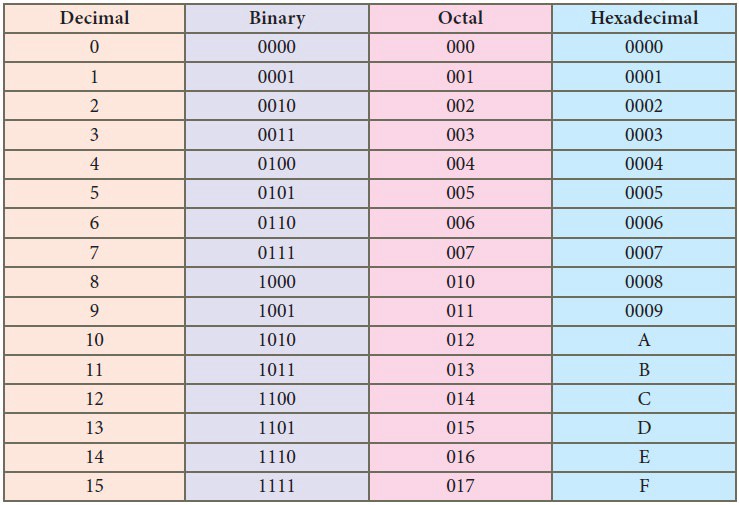
The number system is a way to represent or express numbers. You have heard of various types of number systems such as the whole numbers and the real numbers. But in the context of computers, we define other types of number systems. They are:

  • The decimal number system
  • The binary number system
  • The octal number system and
  • The hexadecimal number system

1. Decimal Number System (Base 10)

In this number system, the digits 0 to 9 represents numbers. As it uses 10 digits to represent a number, it is also called the base 10 number system. Each digit has a value based on its position called place value. The value of the position increases by 10 times as we move from right to left in the number.
For example, the value of 786 is
= 7 x 102 + 8 x 101 + 6 x 100
= 700 + 80 + 6

Binary Number System (Base 2)

A computer can understand only the “on” and “off” state of a switch. These two states are represented by 1 and 0. The combination of 1 and 0 form binary numbers. These numbers represent various data. As two digits are used to represent numbers, it is called a binary or base 2 number system. The binary number system uses positional notation. But in this case, each digit is multiplied by the appropriate power of two based on its position. For example, (101101)2 in decimal is
= 1 x 25 + 0 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20
= 1 x 32 + 0 x 16 + 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1
= 32 + 8 + 4 + 1
= (45)10

Octal Number System (Base 8)

This system uses digits 0 to 7 (i.e. 8 digits) to represent a number and the numbers are as a base of 8.
For example, (24)8 in decimal is
= 2×81+4×80
= (20)10

Hexadecimal Number System (Base 16)

In this system, 16 digits used to represent a given number. Thus it is also known as the base 16 number system. Each digit position represents a power of 16. As the base is greater than 10, the number system is supplemented by letters. Following are the hexadecimal symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F To take A, B, C, D, E, and F as part of the number system is conventional and has no logical or deductive reason.

Units of measurement of data

Machine language is binary. And so it is necessary to discuss how to measure the data stored in a computer. Bit and Byte are the units to measure data.

Bit

The term ‘bit’ is a contraction of the words ‘binary’ and ‘digit’. It is the smallest unit of memory or instruction that can be given or stored on a computer. A bit is either a 0 or a 1. The number in the above example is a 6-bit number as it has 6 binary digits (0s and 1s).

Byte

A group of 8 bits like 01100001 is a byte. Combination of bytes comes with various names like the kilobyte. One kilobyte is a collection of 1000 bytes. A word or letter like ‘A’ or ‘G’ is worth 8 bits or one byte. One thousand bytes make up a kilobyte (one thousand letters approximately). 1024 kilobytes form a Megabyte (Mb) and so on.

Number System Conversion

There are many methods or techniques which can be used to convert numbers from one base to another.

  • Decimal to Binary
  • Decimal to Octal
  • Decimal to Hexadecimal
  • Binary to Decimal
  • Binary to Octal
  • Binary to Hexadecimal
  • Octal to Decimal
  • Octal to Binary
  • Octal to Hexadecimal
  • Hexadecimal to Decimal
  • Hexadecimal to Binary
  • Hexadecimal to Octal

Steps for converting Decimal to Binary

  1. Divide the decimal number to be converted by 2.
  2. Get the remainder from Step 1 as the rightmost digit (least significant digit) of the binary number.
  3. Divide the quotient of the previous divide by 2.
  4. Record the remainder from Step 3 as the next digit (to the left) of the binary number.
    5. Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3. The last remainder thus obtained will be the Most Significant Digit (MSD) of the new base number.
Example:

Convert 2910 to Binary

Step Operation Result Remainder
Step 1 29/2 14 1
Step 2 14/2 7 0
Step 3 7/2 3 1
Step 4 3/2 1 1
Step 5 1/2 0 1

As mentioned in Steps 2 and 4, the remainders have to be arranged in the reverse order so that the first remainder becomes the Least Significant Digit (LSD) and the last remainder becomes the Most Significant Digit (MSD). Decimal Number (29)10 = Binary Number (11101)2.

Steps for converting Decimal to Octal

  1. Divide the decimal number to be converted by 8.
  2. Get the remainder from Step 1 as the rightmost digit (least significant digit) of the octal number.
  3. Divide the quotient of the previous divide by 8.
  4. Record the remainder from Step 3 as the next digit (to the left) of the octal number.
    5. Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3. The last remainder thus obtained will be the Most Significant Digit (MSD) of the new base number.

Steps for converting Decimal to Hexadecimal

  1. Divide the decimal number to be converted by 16.
  2. Get the remainder from Step 1 as the rightmost digit (least significant digit) of the Hexadecimal number.
  3. Divide the quotient of the previous divide by 16.
  4. Record the remainder from Step 3 as the next digit (to the left) of the Hexadecimal number.
    5. Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3. The last remainder thus obtained will be the Most Significant Digit (MSD) of the new base number.

Steps for converting Binary to Decimal

  1. Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the binary system).
  2. Multiply the obtained column values (in Step 1) by the digits in the corresponding columns.
  3. Sum the products calculated in Step 2. The total is the equivalent value in decimal.
Example:

Convert (11101)2 to Decimal

Step Binary Number Decimal Number
Step 1 (11101)2 ((1 × 24) + (1 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10
Step 2 (11101)2 (16 + 8 + 4 + 0 + 1)10
Step 3 (11101)2 (29)10
Binary Number (11101)2 = Decimal Number (29)10

Steps for converting Binary to Octal

  1. Divide the binary digits into groups of three (starting from the right).
  2. Convert each group of three binary digits to one octal digit.
Example:

Convert (11101)2 to Octal

Step Binary Number Octal Number
Step 1 (11101)2 010 101
Step 2 (11101)2 2858
Step 3 (11101)2 (25)8
Binary Number (11101)2 = Octal Number (25)8

Steps for converting Binary to Hexadecimal

  1. Divide the binary digits into groups of four (starting from the right).
  2. Convert each group of four binary digits to one hexadecimal digit.

Steps for converting Octal to Decimal

  1. Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the octal system).
  2. Multiply the obtained column values (in Step 1) by the digits in the corresponding columns.
  3. Sum the products calculated in Step 2. The total is the equivalent value in decimal.

Steps for converting Octal to Binary

  1. Convert each octal digit to a 3 digit binary number (the octal digits may be treated as decimal for this conversion).
  2. Combine all the resulting binary groups (of 3 digits each) into a single binary number.

Steps for converting Octal to Hexadecimal

  1. Convert each octal digit to a 3 digit binary number (the octal digits may be treated as decimal for this conversion).
  2. Combine all the resulting binary groups (of 3 digits each) into a single binary number.
  3. Divide the binary digits into groups of four (starting from the right).
  4. Convert each group of four binary digits to one hexadecimal digit.

Steps for converting Hexadecimal to Binary

  1. Convert each hexadecimal digit to a 4 digit binary number (the hexadecimal digits may be treated as decimal for this conversion).
  2. Combine all the resulting binary groups (of 4 digits each) into a single binary number.

Steps for converting Hexadecimal to Decimal

  1. Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the hexadecimal system).
  2. Multiply the obtained column values (in Step 1) by the digits in the corresponding columns.
  3. Sum the products calculated in Step 2. The total is the equivalent value in decimal.

Steps for converting Hexadecimal to Octal

  1. Convert each hexadecimal digit to a 4 digit binary number (the hexadecimal digits may be treated as decimal for this conversion).
  2. Combine all the resulting binary groups (of 4 digits each) into a single binary number.
  3. Divide the binary digits into groups of three (starting from the right).
  4. Convert each group of three binary digits to one octal digit.
Read More ...

Zeal For Wisdom

Learn Today For Better Tomorrow